>一、单项选择题(>本大题共5>小题，每小题2>分，共10>分)

1.>设f(sin2x)=cos2x+tan2x,0>＜sin2x>＜1,>则f(x)>的表达式为()

A.2x-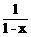,0>＜x>＜1

B.-2x-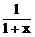,0>＜x>＜1

C.2x-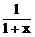,0>＜x>＜1

D.-2x+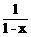,0>＜x>＜1

2.>函数f(x)=sinx>·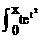dt>在(->∞,+>∞)>上为()

A.>奇函数

B.>偶函数

C.>非奇非偶函数

D.>既是奇函数又是偶函数

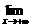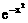
3.>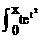［dt>］＝()

A.1

B.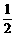

C.2

D.

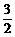
4.>设y=sin(2x+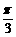)>，则dy>｜x=-=()

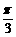A.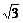dx

B.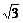

C.dx

D.1

5.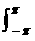x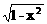cosxdx>＝()

A.-1

B.-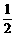

C.0

D.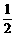

>二、填空题(>本大题共10>小题，每小题2>分，共20>分)

1.>判断f(x)>的增减性：若f(x)>＞0(x>＞0)>，则F(x)=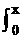f(t)dt>为（）函数.

2.>若f(x)>在x=a>处可导，则n(f(a+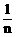)-f(a))=>（）.

3.>当x>→0>时，sinsinx>与ln(1+x)>等价吗（）(>回答“是”或“否”).

4.>函数y=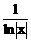>的间断点有x=>（）.

5.>已知函数f(x)>有任意阶导数，且f>′(x)=>［f(x)>］2>，则f(5)(x)=>（）.

6.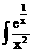dx>＝（）.

7.>已知F(x)>是f(x)>的原函数，则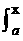f(t+a)dt>＝（）.

8.>设幂级数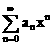>的收敛区间为［-R,R>］(0>＜R>＜+>∞)>，则级数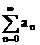(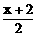)n>的收敛区间为（）.

9.>设z=f(ax+by),f>可微，则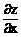>与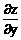>的关系为（）.

10.>方程xlnx>·y>′=y>的通解为（）.

>三、计算题（一）(>本大题共6>小题，每小题6>分，共36>分)

1.>求极限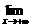

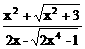
2>．设f(x)=sinx,g(x)=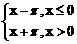>，判断在点x=0>处f(g(x))>的连续性.

3>．设y=f(ex)ef(x)>，其中f(x)>可导且f(0)=f>′(0)=1,f(1)=-1,f>′(1)=0>，求y>′x>｜x=0.

4.>计算二重积分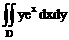>，其中D>是由直线y=1,x+y-3=0,x-y+3=0>围成的图形.

5>．利用敛散性判别法判断级数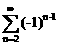>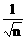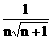［+>］是绝对收敛，还是条件收敛或是发散.

6>．求微分方程dy=ky(N-y)dx(N,k>＞0>为常数)>的解.

>四、计算题（二）(>本大题共2>小题，每小题7>分，共14>分)

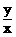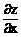1>．设z=xy+xsin>，求x+y.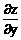

2>．计算二重积分I=.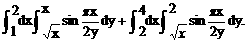

>五、应用题(>本大题共2>小题，每小题8>分，共16>分)

1>．将抛物线y=x2-ax>在直线x=0>与直线x=c>（c>＞a>＞0>）之间的弧段绕x>轴旋转，问当c>固定，a>取何值时所得旋转体体积最小？并求出这个最小值.

2>．已知某产品的需求函数为P=12-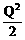>，成本函数为C=100+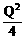>，求产量为多少时总利润最大？并验证是否符合最大利润原则？（P>表示商品价格，Q>为商品数量，C>为总成本）.

>六、证明题（本大题4>分）

>设函数f(x)>连续，证明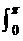xf(sinx)dx=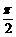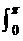f(sinx)dx.